✅ Para calcular la forma polar de un número complejo: halla su módulo con √(a²+b²), luego el ángulo con arctan(b/a). ¡Fácil y rápido!
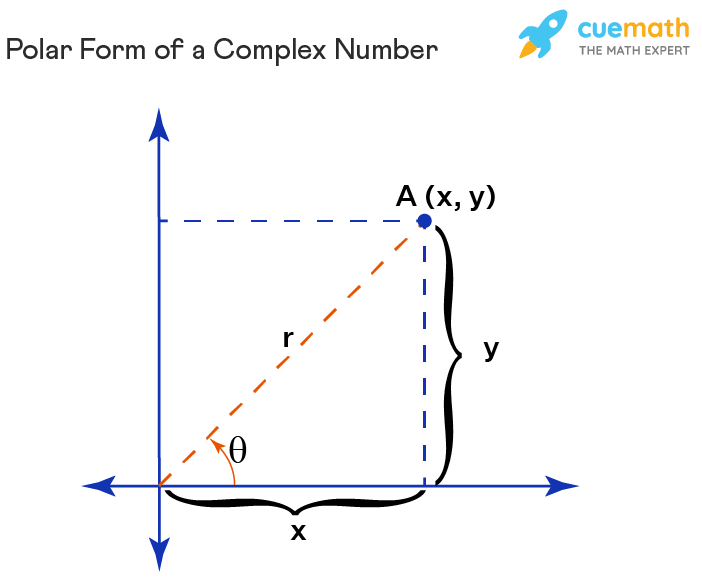
La forma polar de un número complejo se calcula representando dicho número en términos de su módulo y su argumento. Esto implica expresar el número complejo z = a + bi (en forma rectangular) como z = r(cos θ + i sen θ), donde r es el módulo y θ es el argumento. Esta transformación facilita operaciones como multiplicaciones, divisiones y potencias de números complejos.
Te vamos a explicar paso a paso cómo calcular la forma polar de cualquier número complejo, desde la identificación de sus componentes rectangulares hasta el cálculo preciso de su módulo y argumento. Además, aprenderás a interpretar y utilizar la información en formato polar para resolver diversos problemas matemáticos relacionados con números complejos.
¿Qué es la forma polar de un número complejo?
Un número complejo se puede expresar en dos formas principales: rectangular y polar. Mientras que la forma rectangular es z = a + bi, donde a es la parte real y b la parte imaginaria, la forma polar representa este número en términos de su distancia al origen y su ángulo con el eje real.
Se define como:
z = r (cos θ + i sen θ)
- r: módulo o magnitud, que indica la distancia desde el origen hasta el punto (a, b).
- θ: argumento o ángulo, que mide la inclinación del vector que une el origen con el punto (a, b) respecto al eje real positivo.
Paso 1: Calcular el módulo (r)
El módulo de un número complejo se calcula con la fórmula:
r = √(a² + b²)
- a es la parte real.
- b es la parte imaginaria.
Esto equivale a encontrar la distancia desde el punto (a, b) hasta el origen en el plano complejo.
Ejemplo:
Si z = 3 + 4i, entonces:
r = √(3² + 4²) = √(9 + 16) = √25 = 5
Paso 2: Calcular el argumento (θ)
El argumento es el ángulo que forma el vector con el eje real positivo y se calcula mediante:
θ = arctan (b / a)
Sin embargo, hay que prestar atención al cuadrante donde se encuentra el número complejo para obtener el valor correcto de θ.
Recomendaciones para calcular el argumento correctamente:
- Si a > 0, θ = arctan(b/a).
- Si a < 0 y b ≥ 0, θ = arctan(b/a) + π.
- Si a < 0 y b < 0, θ = arctan(b/a) – π.
- Si a = 0 y b > 0, θ = π/2.
- Si a = 0 y b < 0, θ = -π/2.
Ejemplo:
Para z = 3 + 4i, el argumento es:
θ = arctan(4/3) ≈ 0,927 radianes (53,13°)
Paso 3: Escribir el número complejo en forma polar
Con los valores de r y θ calculados, se expresa el número complejo como:
z = r (cos θ + i sen θ)
En el ejemplo, z = 3 + 4i pasa a ser:
z = 5 (cos 0,927 + i sen 0,927)
También es común utilizar la notación con exponentes complejos empleando la fórmula de Euler:
z = r e^{iθ}
En este caso:
z = 5 e^{i 0,927}
Aplicaciones y ventajas de la forma polar
Trabajar con los números complejos en forma polar suele ser muy útil para operaciones como:
- Multiplicación: se multiplican los módulos y se suman los argumentos.
- División: se dividen los módulos y se restan los argumentos.
- Potenciación: se eleva el módulo a la potencia y se multiplica el argumento por la potencia.
- Raíces: se calculan distribuyendo los argumentos de forma adecuada.
Estas propiedades facilitan muchos cálculos trigonométricos y la representación geométrica de números complejos en el plano.
Preguntas frecuentes
¿Qué es la forma polar de un número complejo?
¿Cómo se calcula el módulo de un número complejo?
¿Cómo se determina el argumento de un número complejo?
| Paso | Descripción | Fórmula o Nota |
|---|---|---|
| 1 | Identificar la parte real y la parte imaginaria | z = a + bi, donde a es real y b es imaginaria |
| 2 | Calcular el módulo | r = √(a² + b²) |
| 3 | Calcular el argumento (ángulo) | θ = arctan(b/a), considerar el cuadrante |
| 4 | Expresar en forma polar | z = r(cos θ + i sen θ) o r e^(iθ) |
| 5 | Interpretar el resultado | r es la distancia al origen y θ es el ángulo con el eje real |
¿Te quedó alguna duda? Dejá tus comentarios y no te olvides de revisar otros artículos en nuestra web que te pueden interesar sobre números complejos y matemáticas.