Qué significa que un límite tienda a infinito en matemáticas ✅

✅ Un límite que tiende a infinito indica que la función crece sin control, alcanzando valores muy grandes, revelando comportamiento extremo y esencial.

En matemáticas, que un límite tienda a infinito significa que al aproximarnos a un determinado valor, la función o la expresión evaluada crece sin acotarse, aumentando su valor de manera indefinida. En otras palabras, a medida que la variable independiente se acerca a cierto punto (o a infinito mismo), el resultado de la función se hace arbitrariamente grande, sin estar limitado por ningún número finito.

Este concepto es fundamental para entender el comportamiento de funciones y sucesiones en el análisis matemático y es crucial para muchas áreas como el cálculo, la física y la ingeniería. En el siguiente artículo, profundizaremos en qué implica exactamente que un límite tienda a infinito, cómo se interpreta en distintos contextos y ejemplos prácticos que ilustran este fenómeno, en particular cómo se representa y qué condiciones deben cumplirse para que un límite sea infinito.

¿Qué significa un límite que tiende a infinito?

Cuando hablamos de un límite que «tiende a infinito», nos referimos a la situación en la que el valor de una función crece sin límite a medida que la variable se acerca a un valor específico o también cuando la variable misma tiende a infinito. Formalmente, decimos que:

Lim x→a f(x) = ∞ si para cada número muy grande M > 0, existe una δ > 0 tal que para todos los x que cumplen 0 < |x - a| < δ, se cumple f(x) > M.
Similarmente, cuando lim x→∞ f(x) = ∞, significa que para cualquier número M > 0, existe un N tal que para todos los x > N, f(x) > M.

Esto indica que la función no tiene un valor finito al que se acerque, sino que su valor se incrementa sin límite.

Qué incluye el resumen de Boquitas Pintadas por cada entrega

Contextos comunes de límites que tienden a infinito

1. Límites con variable que tiende a un punto finito

Por ejemplo, consideremos la función f(x) = 1/(x – 2). Al evaluar el límite cuando x se acerca a 2, observamos que:

Si x se acerca a 2 por la derecha (x → 2⁺), 1/(x-2) crece positivamente sin límite, entonces lim x→2⁺ 1/(x – 2) = ∞.
Si x se acerca a 2 por la izquierda (x → 2⁻), 1/(x-2) tiende a −∞.

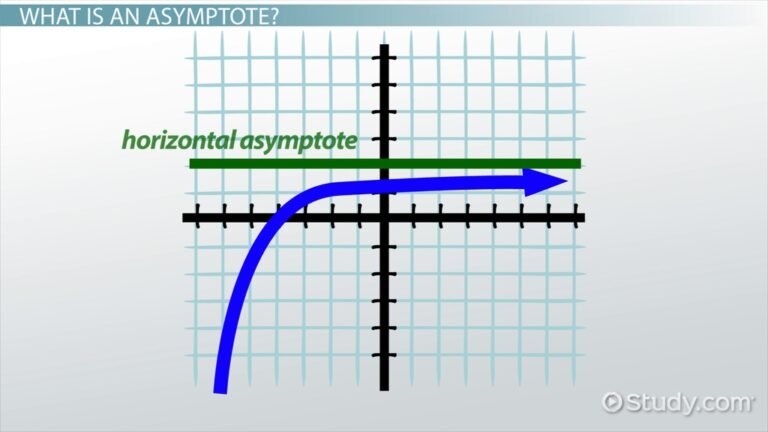
Esto implica que la función presenta una asíntota vertical en x=2 y el valor de la función es cada vez más grande en magnitud a medida que x se acerca a ese valor.

2. Límites con variable que tiende a infinito

Cuando x tiende a infinito, por ejemplo en f(x) = 2x + 3, el valor de la función también tiende a infinito:

lim x→∞ (2x + 3) = ∞

Esto significa que si seguimos aumentando el valor de x, el valor de f(x) seguirá creciendo sin acotarse.

Representación gráfica y propiedades

En la gráfica de la función, que un límite tienda a infinito se representa porque la curva se eleva o cae sin límite en la cercanía del punto de interés, o conforme la variable independiente se va alejando hacia la derecha (x → ∞) o hacia la izquierda (x → −∞).

Observaciones clave:

Un límite infinito no implica que el límite exista en el sentido tradicional, ya que no se acerca a un valor finito.
Indica una comportamiento asintótico, usualmente relacionado con asíntotas verticales (cuando se acerca a un punto finito) o con la tendencia creciente / decreciente de la función (cuando x → ±∞).
El símbolo ∞ es una abstracción que representa comportamiento sin cota, no un número.

Cuáles Son Las Funciones Clave Del Equipo Directivo En Una Escuela

Ejemplos prácticos para entender límites que tienden a infinito

Función	Límite	Resultado	Interpretación
f(x) = 1/(x – 3)	lim x→3⁺ f(x)	∞	La función crece sin límite al acercarse a x=3 desde la derecha.
g(x) = 5x² + 2	lim x→∞ g(x)	∞	Al aumentar x, g(x) crece sin límite.
h(x) = -2x	lim x→-∞ h(x)	∞	Al ir x a -∞, h(x) crece sin límite hacia +∞ (porque está multiplicado por -2).

Consejos para interpretar límites infinitos

Analizá el comportamiento de la función cerca del punto de interés. mirá si los valores crecen o disminuyen sin límite.
Identificá asíntotas verticales para puntos donde la función no está definida o «explota».
Utilizá gráficos para visualizar cómo se comporta la función en los extremos o cerca de puntos problemáticos.
Recordá que un límite infinito describe tendencia, no un valor finito alcanzado.

Preguntas frecuentes

¿Qué es un límite en matemáticas?

Es el valor al que se aproxima una función cuando la variable independiente se acerca a un punto.

¿Qué significa que un límite tienda a infinito?

Indica que la función crece sin acotarse en valor cuando la variable se acerca a un punto o a infinito.

¿Cómo se interpreta un límite infinito en una gráfica?

La curva se aleja hacia arriba o abajo sin tocar un valor fijo en el eje vertical.

Punto clave	Descripción
Definición de límite	Valor al que se aproxima una función al acercarse la variable a un punto.
Límite tending to infinity	La función no se aproxima a un número finito, sino que aumenta o disminuye sin límite.
Notación	(lim_{x to a} f(x) = infty) indica que f(x) crece sin cota al acercarse a a.
Límite en el infinito	Estudia el comportamiento de la función cuando x tiende a (infty) o (-infty).
Límites infinitos y asíntotas	Cuando el límite es infinito, suele haber una asíntota vertical.
Interpretación gráfica	La gráfica se aleja sin límite hacia arriba o abajo, sin acercarse a un punto fijo.
Ejemplo clásico	(lim_{x to 0^+} frac{1}{x} = infty).
Aplicaciones	Se usan para entender comportamiento de funciones, discontinuidades y tipos de crecimiento.