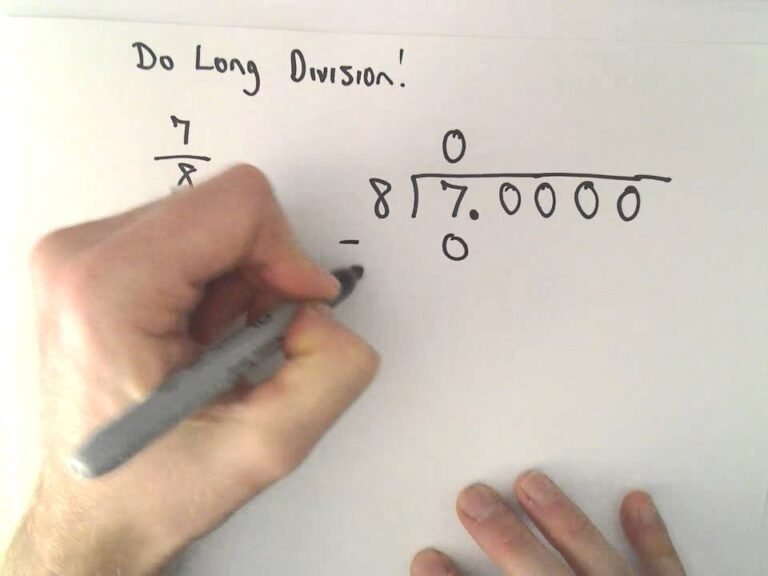Cómo Convertir Una Fracción A Número Decimal Fácilmente
✅ Convierte fracciones a decimales fácil: divide numerador por denominador con calculadora. Método rápido, preciso, ideal para estudiar o finanzas.
Convertir una fracción a número decimal es un proceso sencillo que se realiza dividiendo el numerador por el denominador. Esta operación básica permite expresar cualquier fracción como un número decimal exacto o periódico, facilitando su comprensión y uso en diferentes contextos matemáticos y prácticos.
En este artículo repasaremos paso a paso cómo transformar una fracción en un número decimal de manera clara y práctica. Además, exploraremos distintos casos, consejos y ejemplos para que puedas aplicar esta conversión fácilmente tanto en la escuela como en tu vida diaria.
¿Qué es una fracción y cómo se relaciona con los números decimales?
Una fracción representa una parte de un todo e indica cuántas partes iguales tomamos del total. Se compone de dos números: el numerador (arriba) indica cuántas partes consideramos, y el denominador (abajo) muestra en cuántas partes iguales está dividido el todo.
Por otro lado, un número decimal es una expresión numérica basada en el sistema decimal que utiliza la coma para separar la parte entera de la parte fraccionaria.
Convertir una fracción a decimal implica calcular cuánto equivale esa fracción en términos de décimas, centésimas, milésimas, etc., dependiendo de la precisión deseada.
Pasos para convertir una fracción a número decimal
Identificar el numerador y denominador: Por ejemplo, en la fracción 3/4, el numerador es 3 y el denominador es 4.
Dividir el numerador entre el denominador: Realiza la división 3 ÷ 4 usando la calculadora o procedimiento manual.
Interpretar el resultado: El cociente resultante será el número decimal equivalente a esa fracción.
Siguiendo el ejemplo, al dividir 3 entre 4 obtenemos 0,75, que es el decimal exacto de la fracción 3/4.
Ejemplo práctico
Fracción
Numerador
Denominador
División
Decimal resultante
1/2
1
2
1 ÷ 2
0,5
7/10
7
10
7 ÷ 10
0,7
5/8
5
8
5 ÷ 8
0,625
Diferencias entre decimales exactos y decimales periódicos
Al convertir fracciones, el resultado decimal puede ser:
Decimal exacto: Tiene una cantidad limitada de cifras decimales que terminan. Ejemplo: 1/4 = 0,25.
Decimal periódico: Se repite un patrón infinito de cifras decimales. Ejemplo: 1/3 = 0,3333… (el 3 se repite).
En el caso de decimales periódicos, se puede representar con una barra encima del dígito o grupo que se repite.
Consejos para convertir fracciones complejas
Simplificar la fracción antes de realizar la división para facilitar el cálculo.
Usar una calculadora científica si la división resulta muy larga o para asegurar precisión.
Para fracciones con denominadores que son potencias de 10 (10, 100, 1000), simplemente se coloca la coma decimal en la posición correcta a partir del numerador.
Por ejemplo, 45/100 equivale a 0,45 sin necesidad de dividir.
¿Por qué es útil convertir fracciones a decimales?
Expresar fracciones como números decimales es muy útil porque:
Soy Pilar Díaz, investigadora interdisciplinaria enfocada en historia, ciencia y tecnología. Combino análisis riguroso y divulgación clara para aportar perspectivas profundas que enriquecen el debate sobre educación, sociedad y medioambiente. Mi objetivo es generar conocimiento útil y accesible.
