✅ Aprendé a hacer un análisis completo de una función: dominio, rango, continuidad, derivadas, extremos y gráficos claros paso a paso. ¡Fundamental y fácil!
Realizar un análisis completo de una función implica estudiar sus características principales para comprender su comportamiento en diferentes intervalos y puntos críticos. Esto incluye determinar el dominio, hallar los puntos críticos, analizar la monotonicidad, identificar máximos y mínimos locales, examinar la concavidad y los puntos de inflexión, y finalmente, esbozar su gráfica.
En este artículo te guiaré paso a paso para hacer un análisis exhaustivo de cualquier función, presentando cada etapa de manera clara y estructurada, con ejemplos para que puedas aplicar el método sin inconvenientes. Al finalizar, tendrás todas las herramientas para interpretar y representar funciones de forma precisa y efectiva.
1. Determinar el dominio de la función
El primer paso consiste en identificar el conjunto de valores x para los cuales la función está definida.
- Si la función es una racional, se debe excluir los valores que hacen que el denominador sea cero.
- En funciones con raíces, hay que asegurarse de que el radicando sea mayor o igual a cero si la raíz es de índice par.
- En funciones logarítmicas, el argumento del logaritmo debe ser mayor a cero.
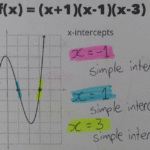
2. Calcular los valores notables y puntos de corte con los ejes
Es clave encontrar los puntos donde la gráfica intersecta los ejes:
- Corte con eje y: Evaluar la función en x = 0.
- Corte con eje x: Resolver la ecuación f(x) = 0 para hallar las raíces.
3. Encontrar la derivada para analizar crecimiento y decrecimiento
La primera derivada (f'(x)) indica dónde la función crece o decrece:
- Calcular f'(x).
- Determinar los puntos críticos resolviendo f'(x) = 0 o donde la derivada no exista.
- Analizar el signo de f'(x) en los intervalos definidos por los puntos críticos para identificar dónde la función es creciente (f'(x) > 0) o decreciente (f'(x) < 0).
4. Identificar máximos y mínimos locales
Con la información de la derivada primera podemos encontrar extremos relativos:
- Si la derivada cambia de positiva a negativa en un punto crítico, hay un máximo local.
- Si cambia de negativa a positiva, hay un mínimo local.
- También se puede usar la segunda derivada para la prueba de la concavidad en esos puntos.
5. Estudiar la concavidad y puntos de inflexión con la segunda derivada
La segunda derivada (f»(x)) proporciona información sobre la forma de la gráfica:
- f»(x) > 0: La función es cóncava hacia arriba.
- f»(x) < 0: La función es cóncava hacia abajo.
- Los puntos donde f»(x) = 0 y cambia de signo son puntos de inflexión, donde la concavidad cambia.
6. Análisis de asíntotas y comportamiento en el infinito
Es importante verificar si la función tiene asíntotas:
- Asíntotas verticales: Ocurren en valores donde la función tiende a infinito sin valor marcado.
- Asíntotas horizontales: Se analizan los límites cuando x → ±∞ para determinar si la función se aproxima a un valor constante.
- Asíntotas oblicuas: Se hallan si el límite al infinito es infinito, pero la función se acerca a una recta inclinada.
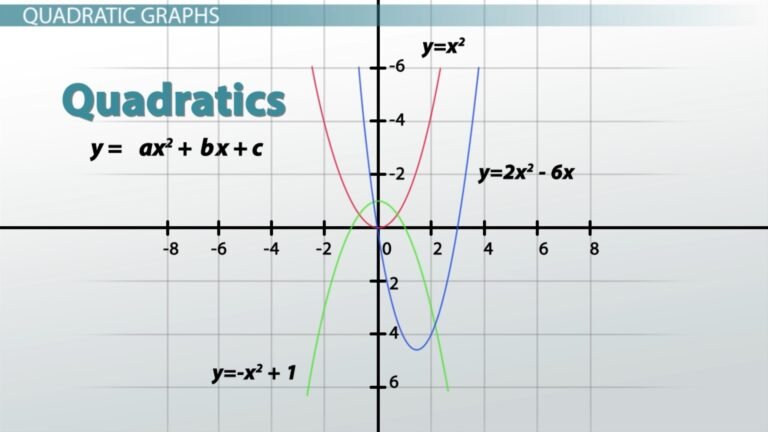
7. Esbozar la gráfica de la función
Una vez que recopilamos toda la información anterior, podemos dibujar un bosquejo que refleje correctamente el comportamiento de la función:
- Ubicar los cortes con los ejes y los puntos críticos.
- Indicar los intervalos de crecimiento y decrecimiento.
- Marcar los máximos y mínimos locales.
- Representar la concavidad y puntos de inflexión.
- Dibujar las asíntotas y mostrar el límite de la función en infinito.
Ejemplo práctico
Para entender mejor el proceso, podemos hacer un análisis completo de una función como f(x) = x³ – 3x² + 2 siguiendo cada paso descrito.
Si querés aprender a hacer este análisis con ejemplos prácticos y detallados, continuá leyendo el artículo completo.
Preguntas frecuentes
¿Qué es un análisis completo de una función?
¿Por qué es importante el análisis de funciones?
¿Qué herramientas matemáticas necesito usar?
| Paso | Descripción | Clave |
|---|---|---|
| 1. Definición y dominio | Determinar para qué valores de x está definida la función. | Evitar valores que causen indefinición o división por cero. |
| 2. Continuidad y límites | Verificar puntos de discontinuidad y comportamiento en el infinito. | Identificar límites laterales y posibles asíntotas. |
| 3. Derivada primera | Calcular y analizar para encontrar intervalos de crecimiento y decrecimiento. | Resolver f'(x)=0 para puntos críticos. |
| 4. Derivada segunda | Determinar la concavidad y puntos de inflexión. | f»(x)>0 concava hacia arriba, f»(x)<0 hacia abajo. |
| 5. Encontrar extremos | Identificar máximos y mínimos locales con la derivada. | Evaluar f(x) en puntos críticos. |
| 6. Asíntotas | Calcular verticales, horizontales y oblicuas mediante límites. | Importante para entender comportamiento extremo. |
| 7. Esbozo de gráfica | Combinar toda información para dibujar la función. | Visualizar forma general y características. |
¿Te sirvió esta guía para entender mejor cómo analizar funciones? Dejá tus comentarios y no te pierdas otros artículos de nuestra web relacionados con matemáticas y ciencias.