✅ Para graficar una función polinómica, identifica coeficientes, encuentra raíces, calcula valores clave, traza puntos y dibuja la curva suave. ¡Fácil y efectivo!
Para graficar una función polinómica paso a paso, es fundamental entender primero su forma, evaluar puntos claves y luego conectarlos para visualizar su comportamiento. El proceso incluye identificar el grado del polinomio, calcular las raíces o ceros, encontrar puntos críticos (máximos, mínimos y puntos de inflexión) y luego realizar un análisis para bosquejar la curva correctamente.
Te guiaré a través de cada etapa para graficar cualquier función polinómica de forma clara y ordenada. Veremos desde cómo encontrar los valores que interceptan el eje x y y, hasta cómo determinar el comportamiento general del polinomio para crear una gráfica precisa a mano o con tecnología. Esta guía te servirá para entender mejor las funciones y mejorar tu habilidad para interpretarlas visualmente.
1. Identificación de la función polinómica
Antes de graficar, asegurate de tener la función polinómica expresada correctamente, por ejemplo: f(x) = 2x³ – 5x² + 3x – 1. El grado del polinomio es el exponente más alto de la variable.
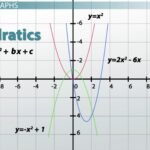
- Grado 1: función lineal.
- Grado 2: función cuadrática.
- Grados superiores: polinomios cúbicos, cuárticos, etc.
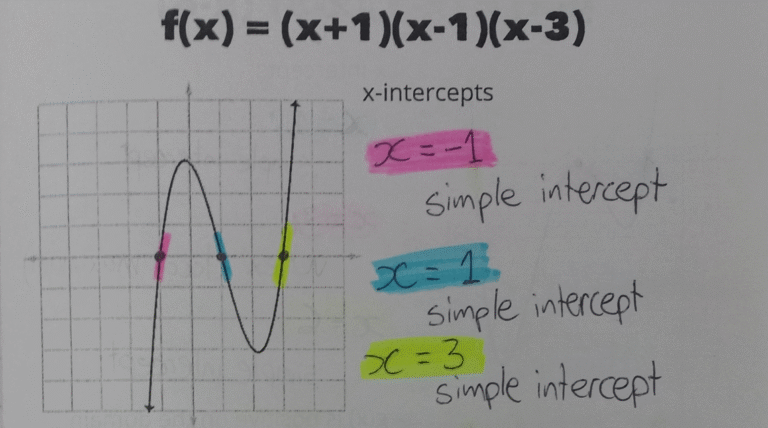
2. Encontrar las raíces o ceros de la función
Las raíces son los valores de x que hacen que f(x)=0. Son puntos donde la función cruza el eje x.
Para encontrarlas:
- Plantea la ecuación f(x)=0.
- Resuelve el polinomio por factorización, fórmula general o métodos numéricos si corresponde.
Por ejemplo, para f(x) = x² – 4, factorizamos a (x-2)(x+2)=0 y obtenemos raíces en x=2 y x=-2.
3. Calcular el valor de la función en puntos clave
Además de las raíces, evalúa la función en puntos adicionales para obtener coordenadas que ayuden a formar la gráfica.
- Evalúa f(0) para encontrar el punto de corte con el eje y.
- Elige valores de x a la izquierda y derecha de las raíces para ver cómo se comporta la función.
4. Determinar los puntos críticos (máximos, mínimos y puntos de inflexión)
Para entender la curvatura de la gráfica, derivá la función y hallá los valores de x donde la derivada sea cero (f'(x) = 0), estos son los puntos críticos.
También es útil calcular la segunda derivada para determinar la naturaleza de esos puntos:
- f»(x) > 0: mínimo local.
- f»(x) < 0: máximo local.
- f»(x) = 0: posible punto de inflexión.
5. Bosquejar la gráfica
Finalmente, tenés todos los puntos importantes para dibujar la función:
- Marcá las raíces y puntos de corte.
- Ubicá los máximos, mínimos y puntos de inflexión según los cálculos previos.
- Conectá estos puntos respetando la pendiente y la dirección de la función.
- Considerá el comportamiento de la función para x muy grandes (tendencia al infinito o menos infinito según el grado y coeficiente líder).
Ejemplo práctico
Para graficar f(x) = x³ – 3x² + 2:
- Raíces: resolver x³ – 3x² + 2=0.
- Puntos críticos: derivar f'(x) = 3x² – 6x y resolver 3x² – 6x=0.
- Evaluar puntos clave como f(0), f(1), f(2).
Con esta información, podés dibujar con precisión la función y entender su forma.
Preguntas frecuentes
¿Qué necesito para graficar una función polinómica?
¿Cómo encuentro los puntos para graficar?
¿Qué tipo de funciones polinómicas puedo graficar?
| Paso | Descripción | Consejos |
|---|---|---|
| 1 | Identificar la función polinómica y su grado | Revisar bien los términos y coeficientes |
| 2 | Calcular valores de y para varios x | Elegir x como negativos, cero y positivos para mejor visión |
| 3 | Marcar puntos en el plano cartesiano | Usar papel con cuadrícula o herramienta digital |
| 4 | Unir los puntos con línea suave | Ajustar curvas según la función (por ejemplo, parábolas) |
| 5 | Analizar características especiales | Buscar raíces, máximos, mínimos y comportamiento al infinito |
| 6 | Verificar y ajustar el gráfico si es necesario | Comparar con gráficos hechos con calculadoras o software |
¿Te quedó alguna duda? Dejanos tus comentarios abajo y no te pierdas otros artículos de nuestra web que te pueden interesar.